三角行列

{{出典の明記|date=2017年8月}

数学の一分野線型代数学における三角行列（さんかくぎょうれつ、英: triangular matrix）は特別な種類の正方行列である。正方行列が 下半三角または下三角であるとは主対角線より「上」の成分がすべて零となるときに言い、同様に上半三角または上三角とは主対角線より「下」の成分がすべて零となるときに言う。三角行列は上半または下半三角となる行列のことを言い、また上半かつ下半三角となる行列は対角行列と呼ぶ。

三角行列に関する行列方程式は解くことが容易であるから、それは数値解析において非常に重要である。LU分解アルゴリズムにより、正則行列が下半三角行列 L と上半三角行列 U との積 LU に書くことができるための必要十分条件は、その行列の首座小行列式 (leading principal minor) がすべて非零となることである。

定義と簡単な性質

下三角行列または左三角行列は $L={\begin{bmatrix}\ell _{1,1}&&\cdots &&0\\\ell _{2,1}&\ell _{2,2}&&&\\\ell _{3,1}&\ell _{3,2}&\ddots &&\vdots \\\vdots &\vdots &\ddots &\ddots &\\\ell _{n,1}&\ell _{n,2}&\dotsb &\ell _{n,n-1}&\ell _{n,n}\end{bmatrix}}$ なる形に書ける行列を言い、同様に上三角行列または右三角行列は $U={\begin{bmatrix}u_{1,1}&u_{1,2}&u_{1,3}&\ldots &u_{1,n}\\&u_{2,2}&u_{2,3}&\ldots &u_{2,n}\\\vdots &&\ddots &\ddots &\vdots \\&&&\ddots &u_{n-1,n}\\0&&\cdots &&u_{n,n}\end{bmatrix}}$ の形に書けるものをいう。ここで用いたような、下三角行列を変数 L（left or lower の略）や上三角行列を変数 U（upper の略）または R（right の略）で表す用法が一般的にしばしば用いられる。

上半かつ下半三角な行列は対角行列といい、また三角行列に相似な行列は三角化可能であると言う。

上三角（resp. 下三角）であるという性質は様々な行列演算に関して保たれる:

二つの上（resp. 下）三角行列の和は上（resp. 下）三角行列である;
二つの上（resp. 下）三角行列の積は上（resp. 下）三角行列である;
正則上（resp. 下）三角行列の逆行列は上（resp. 下）三角である;
上（resp. 下）三角のスカラー倍は上（resp. 下）三角である。

これらの事実により、与えられたサイズの上（resp. 下）三角行列の全体は、同じサイズの正方行列の成す結合多元環（行列環）の部分多元環を成すことがわかる。さらに加えて、リー括弧積を交換子 [A, B] ≔ AB − BA を与えれば、同じサイズの正方行列全体の成すリー環の部分リー環としても見ることもできる。この上（resp. 下）三角行列全体の成すリー環は可解リー環であり、またしばしば全行列リー環のボレル部分リー環とも呼ばれる。

上記の記述においては下半と上半を混ぜた演算を行ってはならない（その場合、一般には三角行列にならない）。例えば上三角行列と下三角行列の和は任意の行列となり得るし、下三角行列と上三角行列との積も三角行列でないものになり得る。

特別なクラス

冪単三角行列

主対角成分が全て 1 の三角行列は単三角行列 (unitriangular) という。単位行列は上半単三角かつ下半単三角なる唯一の行列である。

任意の単三角行列は冪単である。上（resp. 下）単三角行列全体の成す集合はリー群を成す。

冪零三角行列

主対角成分が全て零の三角行列は狭義三角行列であるという。任意の狭義三角行列は冪零行列であり、上（resp. 下）三角行列全体の成す集合は冪零リー環 ${\textstyle {\mathfrak {n}}}$ を成す。このリー環はすべての上（resp. 下）三角行列全体の成すリー環 ${\textstyle {\mathfrak {b}}}$ の導来リー環: ${\textstyle {\mathfrak {n}}=[{\mathfrak {b}},{\mathfrak {b}}]}$ であり、かつこのリー環 ${\textstyle {\mathfrak {n}}}$ は上（resp. 下）単三角行列全体の成すリー群のリー環である。

実はエンゲルの定理により、任意の有限次元冪零リー環は狭義上三角行列からなる部分リー環に共軛、すなわち任意の有限次元冪零リー環は狭義上三角行列に同時三角化可能である。

フロベニウス行列

単三角行列が原子的 (atomic; アトミック) とは、ただ一つの列を除いて非対角成分が全て零であるときに言う。そのような行列をフロベニウス行列やガウス行列（ガウス変換行列）などとも呼ぶ。つまり、下半フロベニウス行列は $\mathbf {L} _{i}={\begin{bmatrix}1&&&\cdots &\cdots &&&0\\0&\ddots &&&&&&\\&\ddots &1&&&&&\\\vdots &&0&1&&&&\vdots \\\vdots &&&\ell _{i 1,i}&1&&&\vdots \\&&\vdots &\vdots &0&\ddots &&\\&&&\vdots &\vdots &\ddots &1&\\0&\dotsb &0&\ell _{n,i}&0&\dotsb &0&1\end{bmatrix}}$ という形をしている。フロベニウス行列の逆行列はふたたびフロベニウスで、もとのフロベニウス行列の非対角成分をすべて符号反転したものによって与えられる。

特徴的な性質

正規三角行列は対角行列である。これは正規三角行列 A に対して A*A および AA* の対角成分を見ればわかる。

上三角行列の転置行列は下三角であり、下三角の転置は上三角である。

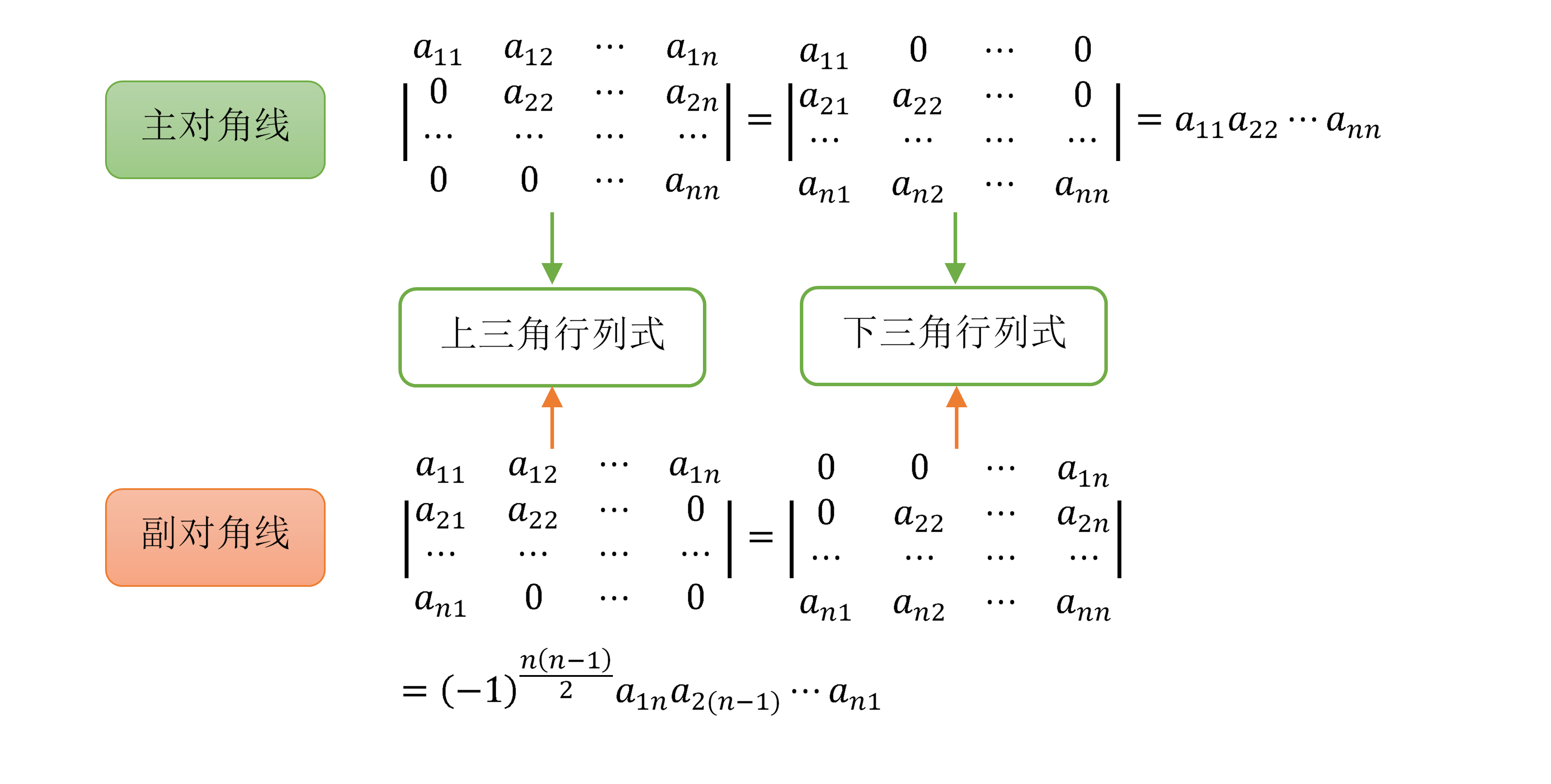
三角行列の行列式は対角成分の積である。任意の三角行列 A に対して λI − A もまた三角行列で、その行列式は A の固有多項式であるから、実は A の対角成分の全体は A の固有値全体の成す多重集合を与える（重複度 m の固有値はちょうど m 個が対角成分に現れる）。

どんな下三角行列もある上三角行列と相似である。より具体的には

{\begin{aligned}&{\begin{bmatrix}&&&1\\&&1&\\&\dots &&\\1&&&\end{bmatrix}}^{-1}{\begin{bmatrix}\ell _{11}&&&\\\ell _{21}&\ell _{22}&&\\\vdots &\vdots &\ddots &\\\ell _{n1}&\ell _{n2}&\dots &\ell _{nn}\end{bmatrix}}{\begin{bmatrix}&&&1\\&&1&\\&\dots &&\\1&&&\end{bmatrix}}\\&\qquad ={\begin{bmatrix}&&&1\\&&1&\\&\dots &&\\1&&&\end{bmatrix}}{\begin{bmatrix}&&&\ell _{11}\\&&\ell _{22}&\ell _{21}\\&\dots &\vdots &\vdots \\\ell _{nn}&\dots &\ell _{n2}&\ell _{n1}\end{bmatrix}}\\&\qquad ={\begin{bmatrix}\ell _{nn}&\dots &\ell _{n2}&\ell _{n1}\\&\ddots &\vdots &\vdots \\&&\ell _{22}&\ell _{21}\\&&&\ell _{11}\end{bmatrix}}\end{aligned}}

となる。同様にして、どんな上三角行列もある下三角行列と相似であることが示せる。したがって、三角化可能性の定義などで相似な行列を考えるときには、一般性を失うことなく議論を三角行列から上三角行列に制限することができる。

三角化可能性

三角行列と相似な行列は三角化可能 (triangularizable) であるという。抽象的には完全旗を固定することに同値である。上三角行列とは標準基底 (e₁, …, e_n) により与えられる標準旗

\langle e_{1}\rangle <\langle e_{1},e_{2}\rangle <\dotsb <\langle e_{1},e_{2},\dotsc ,e_{n-1}\rangle

を保つ行列に他ならない。完全旗は互いに共役なので（一般線形群が基底に推移的に作用するから）、ある完全旗を固定する行列は標準旗を固定する行列と相似である。

任意の複素正方行列は三角化可能である。実際には行列 A が、その固有値すべてを含む体（たとえば代数的閉体）上で三角行列と相似であることが示せる。これは帰納法により証明できる。行列 A は固有ベクトルをもつので、その生成系による商空間を考え、帰納法によって完全旗を固定することを示すことにより、その基底に関して三角化可能であることがわかる。より精密な主張がジョルダン標準形の理論により与えることができ、行列は非常に特別な形の上三角行列（ジョルダン標準形）と相似である。けれども、より単純な三角化で多くの場合は用が足りる。いずれにせよジョルダン標準形の存在を示すときには三角化が必要となる。

複素行列の場合には三角化に関してより強い主張ができる。任意の複素正方行列 A はシューア分解をもつ。つまり A が上三角行列とユニタリ同値（ユニタリ行列による基底変換で相似）である。これは完全旗の正規直交基底をとることで得られる。

代数閉体上の互いに可換な正方行列は同時三角化可能である。

一般化

上三角行列全体の成す集合は結合多元環を成すのであった。これは函数解析学においてヒルベルト空間上のnest algebraに一般化される。

主対角線の上（resp. 下）の成分が全て零の非正方行列は、その非零成分が台形に並ぶから、下（resp. 上）台形行列と呼ばれる。

ボレル部分群とボレル部分環

上（resp. 下）正則三角行列全体の成す集合は群、実際にはリー群を成し、正則行列全体の成す一般線型群の部分群となる。三角行列が可逆となるのはちょうどすべての対角成分が可逆つまり非零となるときであることに注意する。

実係数で考えれば、この群は非連結で、各対角成分が正または負となることに応じて 2ⁿ 個の連結成分を持つ。単位成分は対角成分が全て正の正則三角行列全体に等しく、また正則三角行列全体の成す群はこの単位成分の群と対角線上に ±1 が（各連結成分に対応して）並ぶ対角成分との半直積になる。

正則上三角行列全体の成すリー群に付随するリー環は、必ずしも正則でない上三角行列全体の成す集合であり、それは可解リー環である。これらはそれぞれ、一般線型リー群 GL_n の標準ボレル部分群 B および、一般線型リー環 ${\textstyle {\mathfrak {gl}}_{n}}$ の標準ボレル部分リー環と呼ばれる。

上三角行列はちょうど標準旗を固定する行列である。そのなかで正則三角行列の全体は一般線型群の部分群として、その共軛部分群が適当な完全旗 (complete frag) の固定群として定義されるような群である。これらの部分群はボレル部分群と総称される。正則下三角行列全体の成す群がそのような群であることは、それが標準基底を逆順にしたものに対応する標準旗の固定部分群となることからわかる。

標準旗の適当な部分を忘れて得られる部分旗の固定部分群は、区分行列として上三角な（つまり各区分は上三角であるとは限らない）行列の成す集合として記述することができる。そのような部分群の共軛は適当な部分旗の固定部分群として定義される。これらの部分群を放物型部分群と総称する。

例えば、二次の上単三角行列全体の成す群は係数体の加法群に同型である。複素係数の場合にはその群は放物型メビウス変換からなる群に対応する。三次の上単三角行列の全体はハイゼンベルク群を成す。

注

注釈

出典

参考文献

外部リンク

『上三角行列と下三角行列の意味と6つの定理』 - 高校数学の美しい物語
Weisstein, Eric W. "Trianglular Matrix". mathworld.wolfram.com (英語).
trianglular matrix in nLab
trianglular matrix - PlanetMath.（英語）
Definition:Trianglular Matrix at ProofWiki
Ivanova, O.A. (2001), “Trianglular matrix”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Triangular_matrix

三角行列式和对角行列式Word模板下载_编号lgzpygkx_熊猫办公